Calculating polygon areas is one of the most basic geometric operations. Most GIS analysts using ArcGIS are taught to calculate polygon areas in ArcMap using the Calculate Geometry tool in the attribute table. This allows the calculation of area in the coordinate system of the data source or the coordinate system of the data frame in the desired areal units.
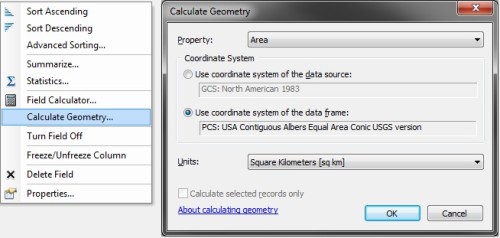
Although this tool fulfills most use cases, it falls short in a number of ways.
- Area calculations are not allowed for feature classes and data frames in geographic coordinate systems. This point is taught in introductory GIS classes as “you must always project data before you can calculate area or perimeter.”
- The area calculation uses a planar/Cartesian method. This produces accurate areas when using an equal-area projected coordinate system such as Albers conic in the above screenshot. But planar calculations with other coordinate systems are less accurate; with geographic coordinate systems, the results are in the useless units of square degrees.
- The Calculate Geometry tool is not available as a standalone geoprocessing tool for use in Model Builder or Python. The Add Geometry Attributes tool is similar, but populates new fields with the desired information instead of an existing field.
My preferred workaround is to use Field Calculator to access this information via the ArcPy geometry objects and the shape field in the attribute table. Using the Python parser in Field Calculator, the following expression returns the geodesic areas of polygon features in square kilometers as floating point numbers:
!Shape!.getArea("GEODESIC","SQUAREKILOMETERS")
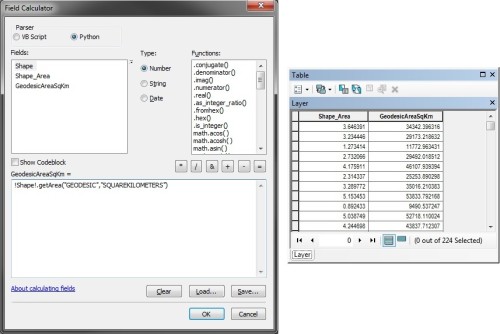
This highly accurate area calculation can be performed on feature classes in geographic coordinate systems (i.e. “unprojected” feature classes). The "GEODESIC" parameter can be substituted for any of the {type} strings discussed below, while the "SQUAREKILOMETERS" parameter can be substituted for any of the {units} strings listed below.
A number of different strings are valid for the {type} parameter in the getArea() method. All but PLANAR account for the curvature of the earth by altering the path of lines lines between vertices. The differences between measurement types become negligible with features that are sufficiently small or have many vertices (i.e. are sufficiently densified).
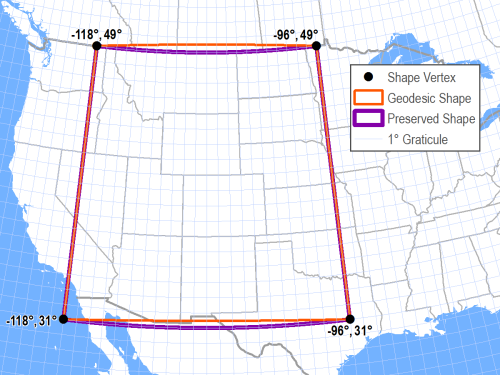
PLANARlines calculate areas without accounting for the curvature of the earth, and utilize simple two-dimensional Cartesian calculations. This method is the fastest, but suffers from the problems discussed above.GEODESIClines are the shortest distance between both points; this is equivalent to the great circle on a spherical datum. This method is the second slowest, but highly accurate. This measurement type is shown as the orange line in the map below.GREAT_ELLIPTIClines intersect the datum and a plane that passes through both points and the spheroid’s center; this is equivalent to a great circle on a spherical datum. This method is the slowest and generally not as useful asGEODESIC.LOXODROMElines follow loxodromes between points, also known as lines of constant bearing or rhumb lines. These lines spiral over long distances, but are simplest for navigation in aviation and boating. This method is the third fastest.PRESERVE_SHAPElines retain their geometric shape. For example, two points with the same latitude would be connected by the circle of latitude with this measurement type; a line with theGEODESICmeasurement type would be shorter but not follow a circle of latitude. This method is the second fastest. This measurement type is shown as the purple line in the map below.
The valid strings for the {units} parameter in the getArea() method include:
ACRESfor acres, equal to 4,046.856 square metersARESfor ares, equal to 100 square metersHECTARESfor hectares, equal to 10,000 square metersSQUARECENTIMETERSfor square centimeters, equal to 0.0001 square metersSQUAREDECIMETERSfor square decimeters, equal to 0.01 square metersSQUAREINCHESfor square inches, equal to 0.00064516 square metersSQUAREFEETfor square feet, equal to 0.092903 square metersSQUAREKILOMETERSfor square kilometers, equal to 1,000,000 square metersSQUAREMETERSfor square metersSQUAREMILESfor square miles, 2,589,988 square metersSQUAREMILLIMETERSfor square millimeters, equal to 0.000001 square metersSQUAREYARDSfor square yards, equal to 0.83612736 square meters
Very helpful thank you so much!
Thank you